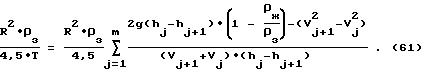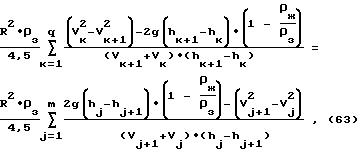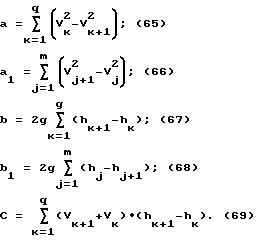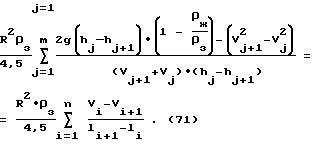Инвестиции
Стартапам
Инвесторам
Инвесторам
Аналитика
Инвестиции
Стартапам
Инвесторам
Аналитика
Спрос и кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Гранты и кредиты
Гранты и кредиты
Инфраструктура
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Патентование
Патентование
Обучение и карьера
Обучение
Карьера
Обучение и карьера
Проекты для мегаполиса
Проекты для мегаполиса
Технологические городские проекты
Проекты для мегаполиса
О Кластере
О Кластере
Лидеры цифровой трансформации
Лидеры цифровой трансформации
Академия инноваторов
Академия инноваторов
Новатор Москвы
Новатор Москвы
Обучение и карьера
Обучение и карьера
Образовательные программы и база знаний
Обучение
Обучение и карьера
Образовательные программы и база знаний


 и ее плотность, отличающийся тем, что, с целью
улучшения метрологических характеристик измерения за счет осуществления измерения при ограниченных по величине скоростях движения зонда, осуществляют разгон зонда до обусловленной по величине и
направлению скорости, измеряют в требуемые моменты времени tj,ti текущие значения высот hj, занятых зондом, и горизонтальной составляющей пути, пройденного зондом,
li или для обусловленных значений высот hj и пути li и измеряют времена их достижения, рассчитывают необходимые промежуточные величины, в частности, средние значения
составляющих скорости движения зонда на соответствующих участках вертикальной Vj и горизонтальной Vi составляющих траектории движения, на основании закона о сохранении энергии и
второго закона Ньютона получают формулы для расчета плотности и вязкости жидкости и рассчитывают для каждого направления движения измеренные значения плотности ρж и вязкости η
жидкости, а результирующие значения вязкости и плотности жидкости оценивают как средние или средневзвешенные значения от их значений по направлениям движения.
и ее плотность, отличающийся тем, что, с целью
улучшения метрологических характеристик измерения за счет осуществления измерения при ограниченных по величине скоростях движения зонда, осуществляют разгон зонда до обусловленной по величине и
направлению скорости, измеряют в требуемые моменты времени tj,ti текущие значения высот hj, занятых зондом, и горизонтальной составляющей пути, пройденного зондом,
li или для обусловленных значений высот hj и пути li и измеряют времена их достижения, рассчитывают необходимые промежуточные величины, в частности, средние значения
составляющих скорости движения зонда на соответствующих участках вертикальной Vj и горизонтальной Vi составляющих траектории движения, на основании закона о сохранении энергии и
второго закона Ньютона получают формулы для расчета плотности и вязкости жидкости и рассчитывают для каждого направления движения измеренные значения плотности ρж и вязкости η
жидкости, а результирующие значения вязкости и плотности жидкости оценивают как средние или средневзвешенные значения от их значений по направлениям движения. и ее плотность по формуле
и ее плотность по формуле
 (2)
(2) среднее значение горизонтальной составляющей скорoсти движения зонда на i-ом участке.
среднее значение горизонтальной составляющей скорoсти движения зонда на i-ом участке. (3)
(3) (4)
(4) (5)
(5)


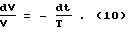


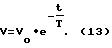

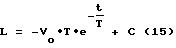
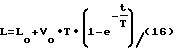
 и Li, подстановкой этих значений в указанные выражения мы получаем уравнения,
характеризующие взаимосвязь других входящих в уравнения величин:
и Li, подстановкой этих значений в указанные выражения мы получаем уравнения,
характеризующие взаимосвязь других входящих в уравнения величин: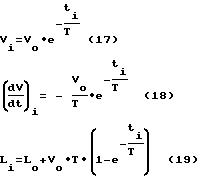
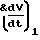 и
и  зонда. В случае применения уравнения (19) необходимо для трех значений времени t1, t2 и t3 измерить пройденные пути L1, L2 и L3.
зонда. В случае применения уравнения (19) необходимо для трех значений времени t1, t2 и t3 измерить пройденные пути L1, L2 и L3.

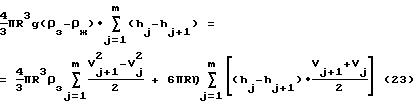

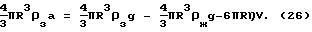



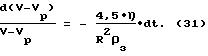



 или четырех значений пройденного при погружении пути
L1, L2, L3 и L4 позволит получить подстановкой их в уравнения (36), (37) и (38) получить системы нелинейных уравнений, решение которых известными способами
позволит определить все неизвестные величины.
или четырех значений пройденного при погружении пути
L1, L2, L3 и L4 позволит получить подстановкой их в уравнения (36), (37) и (38) получить системы нелинейных уравнений, решение которых известными способами
позволит определить все неизвестные величины. Учитывая, что баланс (40) справедлив для каждого из участков вертикальной составляющей движения зонда при всплытии, справедливым
оказывается и следующее равенство (постоянные величины, не зависящие от индекса j вынесены за знаки сумм):
Учитывая, что баланс (40) справедлив для каждого из участков вертикальной составляющей движения зонда при всплытии, справедливым
оказывается и следующее равенство (постоянные величины, не зависящие от индекса j вынесены за знаки сумм):

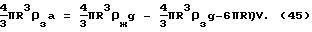



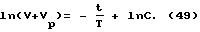
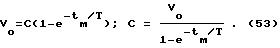
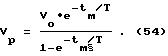
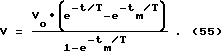
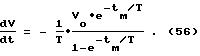

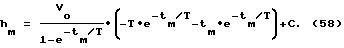

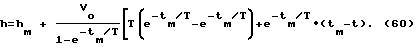
 и
и