Инвестиции
Стартапам
Инвесторам
Инвесторам
Аналитика
Инвестиции
Стартапам
Инвесторам
Аналитика
Спрос и кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Гранты и кредиты
Гранты и кредиты
Инфраструктура
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Патентование
Патентование
Обучение и карьера
Обучение
Карьера
Обучение и карьера
Проекты для мегаполиса
Проекты для мегаполиса
Технологические городские проекты
Проекты для мегаполиса
О Кластере
О Кластере
Лидеры цифровой трансформации
Лидеры цифровой трансформации
Академия инноваторов
Академия инноваторов
Новатор Москвы
Новатор Москвы
Обучение и карьера
Обучение и карьера
Образовательные программы и база знаний
Обучение
Обучение и карьера
Образовательные программы и база знаний



 ; iL - ток дросселя; uс - напряжение на конденсаторе; zk1, zk2 - моменты коммутации в относительно времени на k-том тактовом интервале; Xx-1 - вектор переменных состояния системы в начале k-го тактового интервала;
; iL - ток дросселя; uс - напряжение на конденсаторе; zk1, zk2 - моменты коммутации в относительно времени на k-том тактовом интервале; Xx-1 - вектор переменных состояния системы в начале k-го тактового интервала;  - вектор.
- вектор.

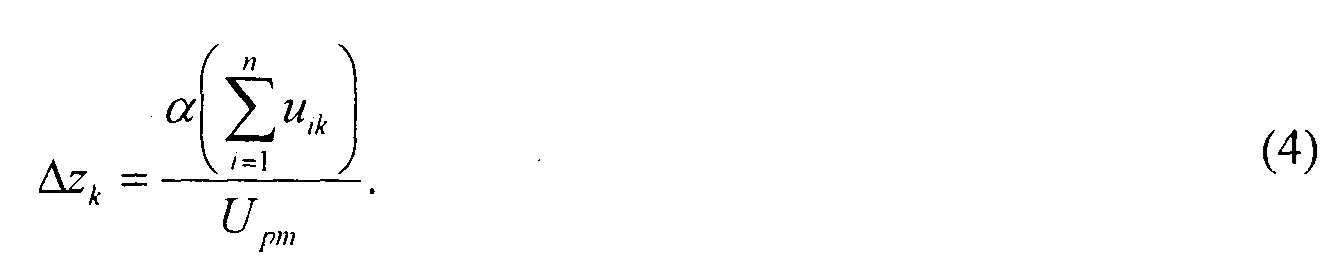
 для импульсной САУ, описываемой СДУ n-го порядка на основе МНЦ, имеет вид
для импульсной САУ, описываемой СДУ n-го порядка на основе МНЦ, имеет вид

 - матрица монодромии стабилизируемого 1-цикла, Yk-1=Хk-1-X'.
- матрица монодромии стабилизируемого 1-цикла, Yk-1=Хk-1-X'.
 ,
,
