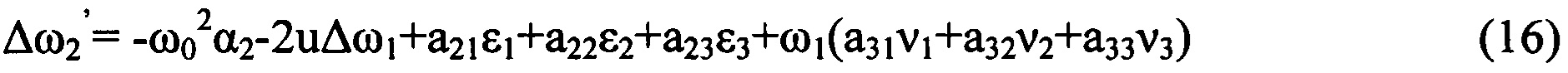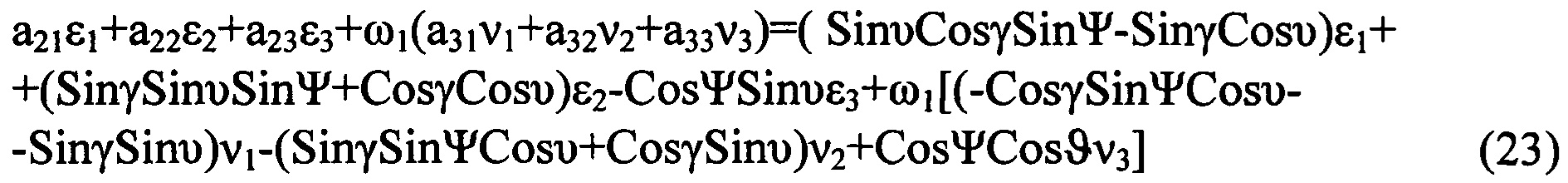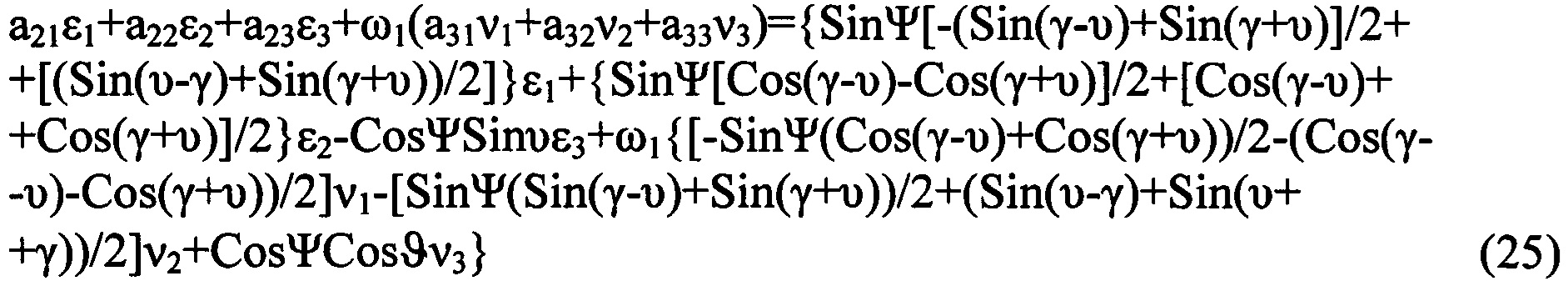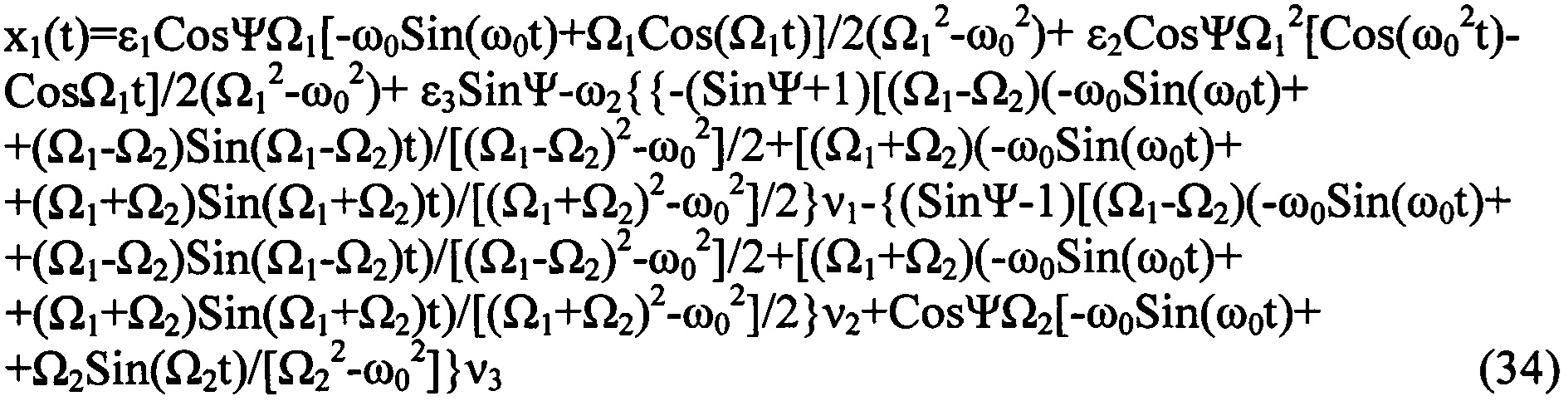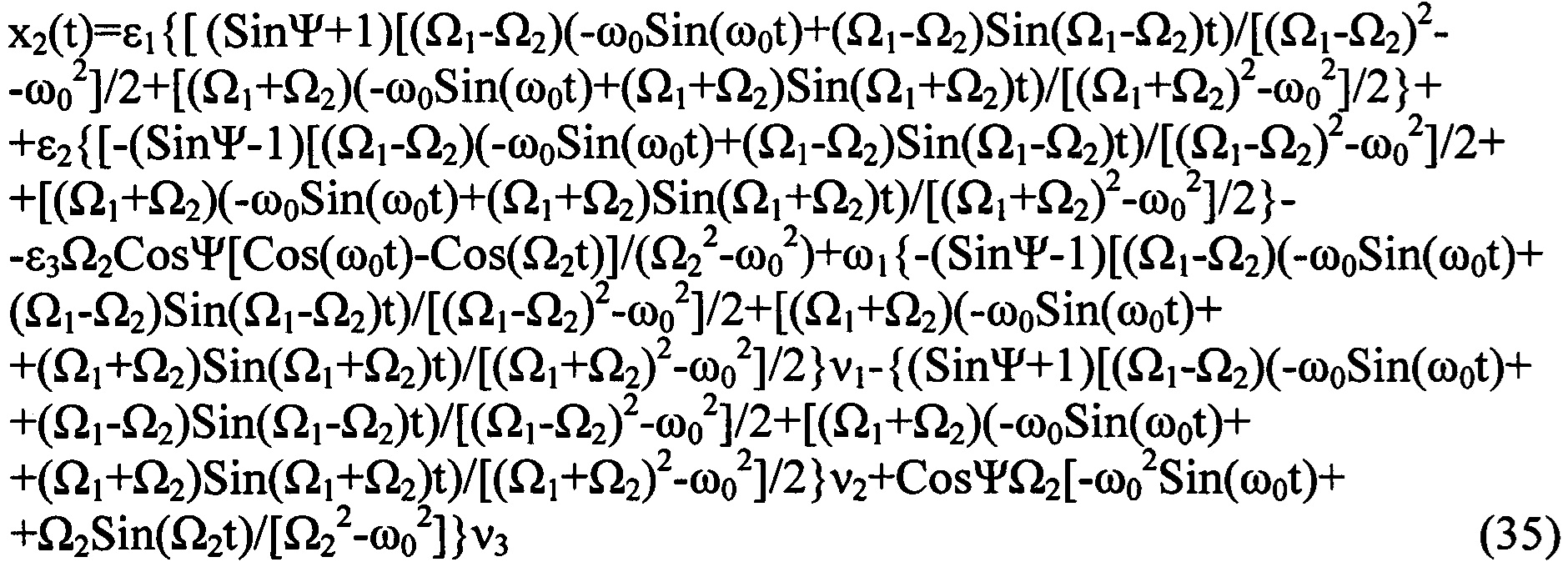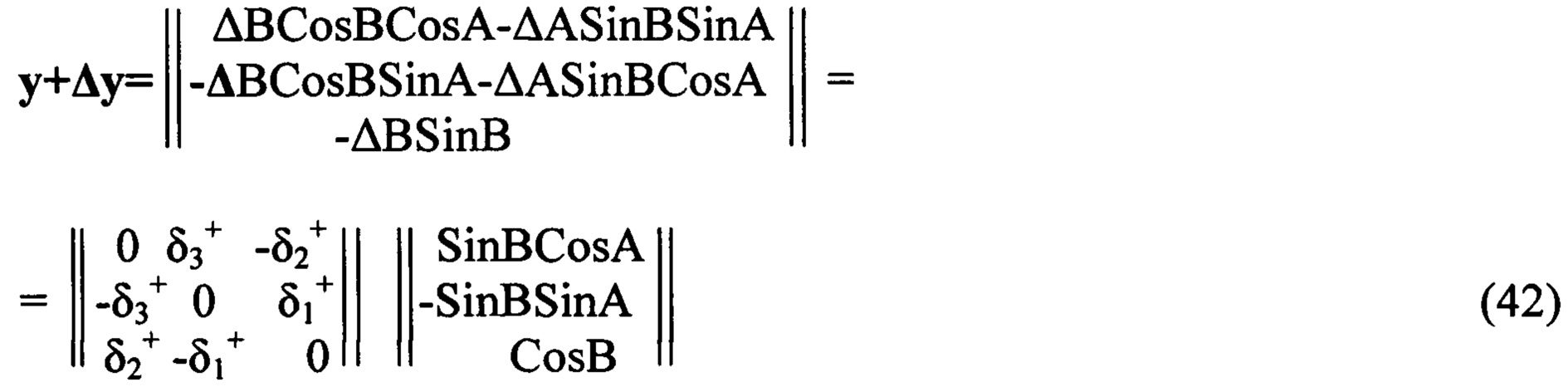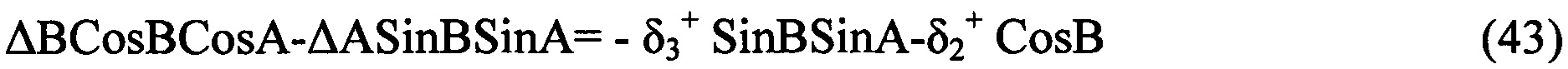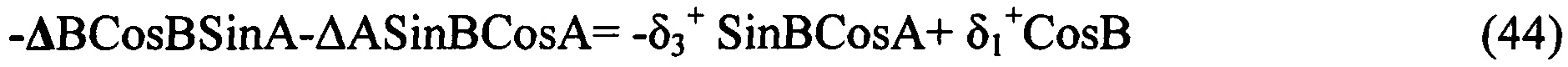Инвестиции
Стартапам
Инвесторам
Инвесторам
Аналитика
Инвестиции
Стартапам
Инвесторам
Аналитика
Спрос и кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Гранты и кредиты
Гранты и кредиты
Инфраструктура
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Патентование
Патентование
Обучение и карьера
Обучение
Карьера
Обучение и карьера
Проекты для мегаполиса
Проекты для мегаполиса
Технологические городские проекты
Проекты для мегаполиса
О Кластере
О Кластере
Лидеры цифровой трансформации
Лидеры цифровой трансформации
Академия инноваторов
Академия инноваторов
Новатор Москвы
Новатор Москвы
Обучение и карьера
Обучение и карьера
Образовательные программы и база знаний
Обучение
Обучение и карьера
Образовательные программы и база знаний













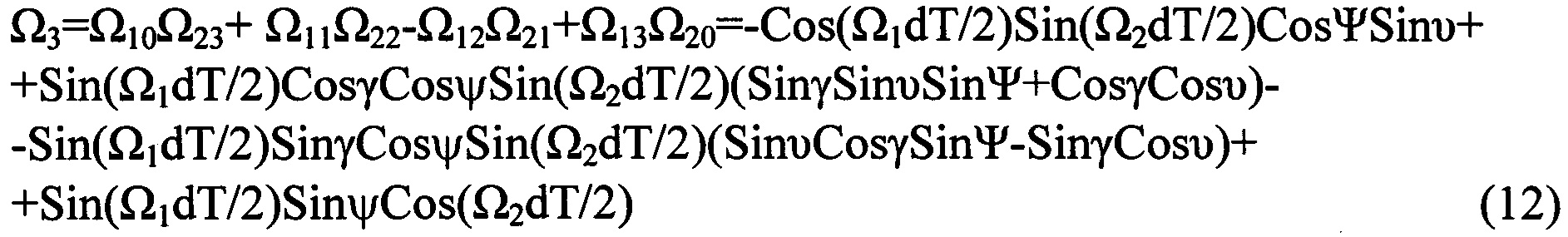
 , получающаяся из кватернионной матрицы
, получающаяся из кватернионной матрицы

 - кососимметрическая матрица, получающаяся из кватернионной матрицы (13) вычеркиванием из нее первого столбца и первой строки; элементы матрицы
- кососимметрическая матрица, получающаяся из кватернионной матрицы (13) вычеркиванием из нее первого столбца и первой строки; элементы матрицы  , i=0, 1, 2, 3 приведены в (9)-(12).
, i=0, 1, 2, 3 приведены в (9)-(12).