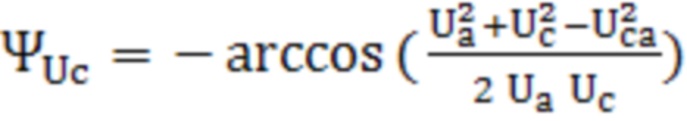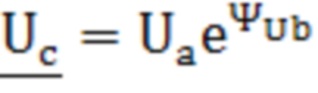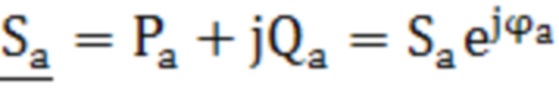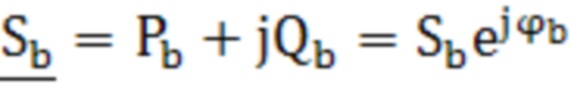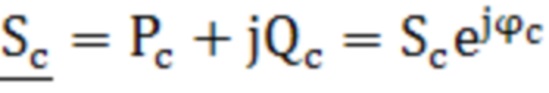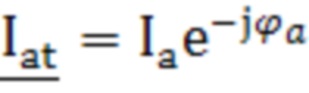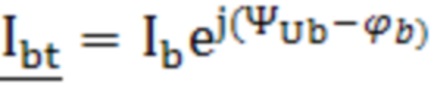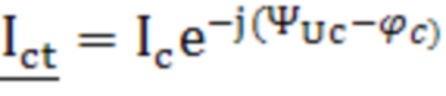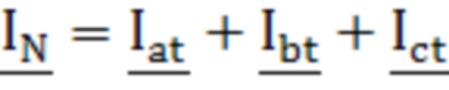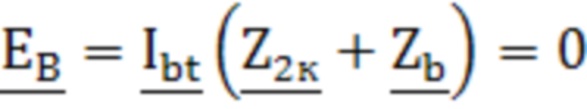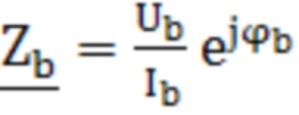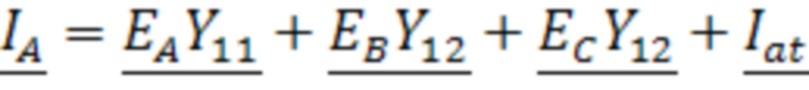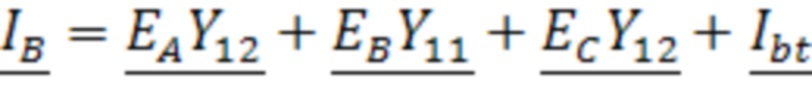Инвестиции
Стартапам
Инвесторам
Инвесторам
Аналитика
Инвестиции
Стартапам
Инвесторам
Аналитика
Спрос и кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Гранты и кредиты
Гранты и кредиты
Инфраструктура
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Патентование
Патентование
Обучение и карьера
Обучение и карьера
Проекты для мегаполиса
Проекты для мегаполиса
Технологические городские проекты
Проекты для мегаполиса
О Кластере
О Кластере
Лидеры цифровой трансформации
Лидеры цифровой трансформации
Академия инноваторов
Академия инноваторов
Новатор Москвы
Новатор Москвы
Обучение и карьера
Обучение и карьера
Образовательные программы и база знаний
Обучение
Обучение и карьера
Образовательные программы и база знаний


 и
и  первичной и вторичной обмоток трансформатора в режиме короткого замыкания, комплексные сопротивления
первичной и вторичной обмоток трансформатора в режиме короткого замыкания, комплексные сопротивления 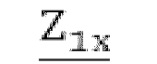 и
и  первичной и вторичной обмоток трансформатора в режиме холостого хода и комплексные проходимости
первичной и вторичной обмоток трансформатора в режиме холостого хода и комплексные проходимости  и
и  характеризующие магнитную систему первичной и вторичной обмоток трансформатора
характеризующие магнитную систему первичной и вторичной обмоток трансформатора ,
,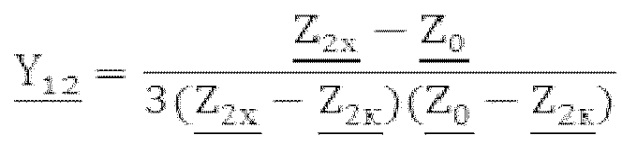 ,
, , где
, где 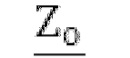 - комплексное сопротивление нулевой последовательности трансформатора. Технический результат: возможность определения параметров математической модели трансформатора со схемой соединения «звезда/звезда-с-нулем», включая комплексные проходимости, характеризующие магнитную систему первичной и вторичной обмоток трансформатора, и комплексное сопротивление, учитывающее размагничивающее действие вихревых токов в баке трансформатора, а также обеспечение сходимости расчетных и измеряемых величин при математическом описании трансформатора. 1 табл., 2 ил.
- комплексное сопротивление нулевой последовательности трансформатора. Технический результат: возможность определения параметров математической модели трансформатора со схемой соединения «звезда/звезда-с-нулем», включая комплексные проходимости, характеризующие магнитную систему первичной и вторичной обмоток трансформатора, и комплексное сопротивление, учитывающее размагничивающее действие вихревых токов в баке трансформатора, а также обеспечение сходимости расчетных и измеряемых величин при математическом описании трансформатора. 1 табл., 2 ил.
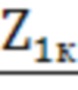 и
и  первичной и вторичной обмоток трансформатора в режиме короткого замыкания, комплексные сопротивления
первичной и вторичной обмоток трансформатора в режиме короткого замыкания, комплексные сопротивления 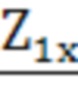 и
и  первичной и вторичной обмоток трансформатора в режиме холостого хода и определяют комплексные проходимости
первичной и вторичной обмоток трансформатора в режиме холостого хода и определяют комплексные проходимости  и
и  , характеризующие магнитную систему первичной и вторичной обмоток трансформатора
, характеризующие магнитную систему первичной и вторичной обмоток трансформатора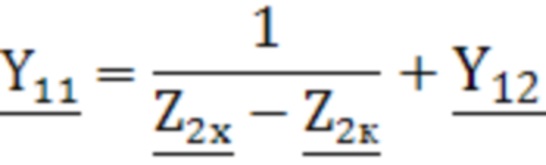 ,
, ,
, ,
,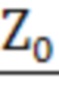 - комплексное сопротивление нулевой последовательности трансформатора.
- комплексное сопротивление нулевой последовательности трансформатора. и
и 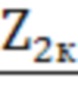 первичной и вторичных обмоток трансформатора в режиме короткого замыкания, комплексных сопротивлений
первичной и вторичных обмоток трансформатора в режиме короткого замыкания, комплексных сопротивлений 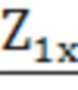 и
и  первичной и вторичной обмоток трансформатора в режиме холостого хода и определение комплексных проходимостей
первичной и вторичной обмоток трансформатора в режиме холостого хода и определение комплексных проходимостей 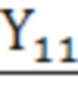 и
и  , характеризующих магнитную систему первичной и вторичной обмоток трансформатора:
, характеризующих магнитную систему первичной и вторичной обмоток трансформатора: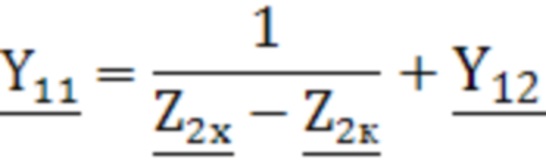

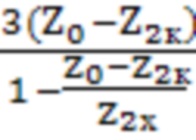
 - комплексное сопротивление нулевой последовательности трансформатора.
- комплексное сопротивление нулевой последовательности трансформатора.