Инвестиции
Стартапам
Инвесторам
Инвесторам
Аналитика
Инвестиции
Стартапам
Инвесторам
Аналитика
Спрос и кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Спрос и кооперация
Развитие и продвижение бизнеса
Спрос
Кооперация
Гранты и кредиты
Гранты и кредиты
Инфраструктура
Инфраструктура
Современные пространства
для бизнеса
для бизнеса
Инфраструктура
Патентование
Патентование
Обучение и карьера
Обучение
Карьера
Обучение и карьера
Проекты для мегаполиса
Проекты для мегаполиса
Технологические городские проекты
Проекты для мегаполиса
Технологические городские проекты
О Кластере
О Кластере
Лидеры цифровой трансформации
Лидеры цифровой трансформации
Академия инноваторов
Академия инноваторов
Новатор Москвы
Новатор Москвы
Обучение и карьера
Обучение и карьера
Образовательные программы и база знаний
Обучение
Обучение и карьера
Образовательные программы и база знаний



 , связанную с Ai соотношениями
, связанную с Ai соотношениями
 малых углов поворота;
малых углов поворота;










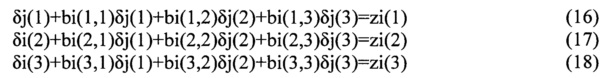



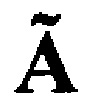 определяется как
определяется как
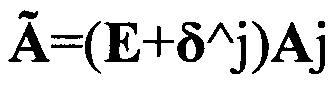 и
и 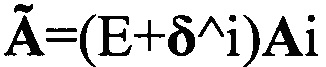 (равно как и матрицы δ^i, δ^j), не являются тождественными и отличаются в общем случае начальной матрицей Aij0 взаимной ориентации, что может оказаться важным в ряде приложений.
(равно как и матрицы δ^i, δ^j), не являются тождественными и отличаются в общем случае начальной матрицей Aij0 взаимной ориентации, что может оказаться важным в ряде приложений.









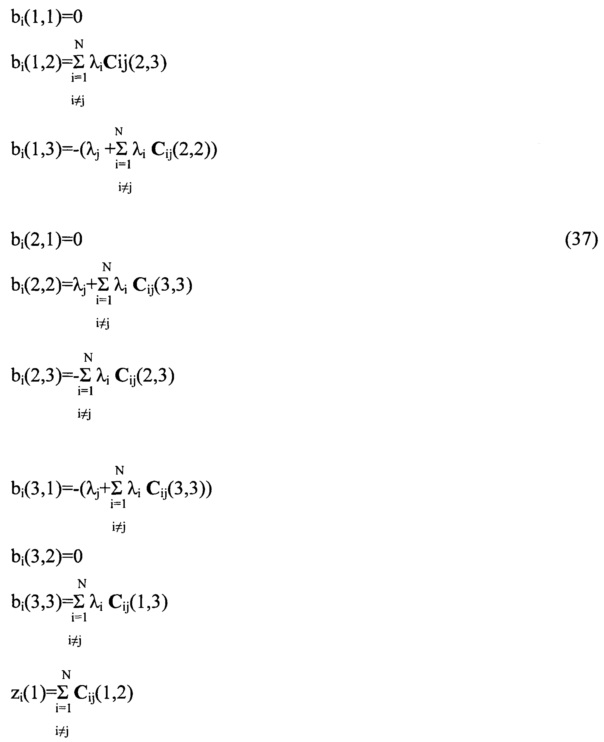








 , которая состоит из последовательно соединенных блока вычисления переменных bi (k, r) (поз. 4), где k, r - номера строк и столбцов матриц ориентации A(k, r) комплексируемых систем, блока вычисления измерений z(i) (поз. 5), блока вычисления невязок δi (поз. 6), блока фильтрации невязок δi (поз. 7) и блока вычисления матрицы ориентации
, которая состоит из последовательно соединенных блока вычисления переменных bi (k, r) (поз. 4), где k, r - номера строк и столбцов матриц ориентации A(k, r) комплексируемых систем, блока вычисления измерений z(i) (поз. 5), блока вычисления невязок δi (поз. 6), блока фильтрации невязок δi (поз. 7) и блока вычисления матрицы ориентации 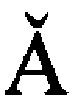 (поз. 8).
(поз. 8).

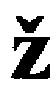 , получаем искомое решение (
, получаем искомое решение (




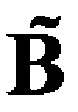 определяется как
определяется как
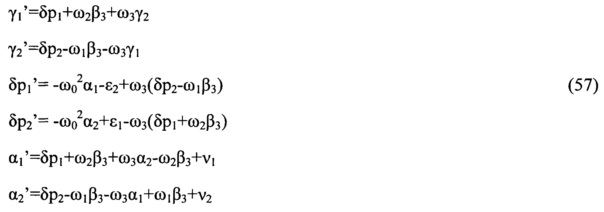



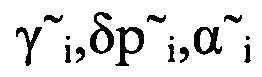 переменных γi, δpi, αi, получаемой на выходе фильтра.
переменных γi, δpi, αi, получаемой на выходе фильтра.






 , и векторы х (64). Компоненты γi векторов х, i=1, 2 используются для коррекции матрицы направляющих косинусов:
, и векторы х (64). Компоненты γi векторов х, i=1, 2 используются для коррекции матрицы направляющих косинусов:

 в осях приборного трехгранника и скорости V1, V2, полученные в блоке обработки первичной информации.
в осях приборного трехгранника и скорости V1, V2, полученные в блоке обработки первичной информации.



